Un puerto, por definición, es un par de terminales a través de las cuales es posible que entre o salga
corriente de una red o un dispositivo. Dispositivos de dos terminales como las resistencias, los condensadores y los inductores son redes de un puerto.
En general, una red puede tener n
puertos. Cada puerto de acceso a la red consta de un par de terminales. La
corriente que entra en una terminal sale a través del otro, de modo que la
corriente neta que entra en un puerto es igual a cero.
De particular relevancia son las las redes de dos puertos, es decir, circuitos (como por ejemplo filtros activos y pasivos y amplificadores) en que se define un par de terminales como puerto de entrada y otro par de terminales como puerto de salida. Una red de dos puertos puede conectarse con un generador o una carga tal y como se muestra, por ejemplo, en la Figura 1. También puede conectarse con otra red de dos puertos para constituir una red de dos puertos más compleja.
 |
| Fig. 1. Red Lineal de 2 Puertos |
siendo v1 e i1 la tensión y la corriente en el puerto “1”, y v2 e i2 la tensión y la corriente en el puerto “2” de la red de dos puertos. Los términos zij representan la relación entre entrada y salida del circuito; en particular, el índice j indica la puerta en que se aplica una señal, mientras que el índice i indica el puerto donde se observa una señal. La red se define simétrica cuando z11= z22, y recíproca cuando z12 = z21.
La matriz [Z] se puede descomponer en dos ecuaciones:
A partir de estas ecuaciones es posible definir el significado de los términos zij de la matriz:
Los términos z11 y z21 se determinan dejando el puerto de salida en circuito abierto (es decir, forzando i2 = 0), y excitando el puerto de entrada con un generador de tensión. Por ello se denominan impedancia de entrada con la salida en circuito abierto e impedancia de transferencia (o transimpedancia) con la salida en circuito abierto, respectivamente.
Los términos z22 y z12 se determinan dejando el puerto de entrada en circuito abierto (es decir, forzando i1 = 0), y excitando el puerto de salida con un generador de tensión. Por ello se denominan impedancia de salida con la entrada en circuito abierto e impedancia de transferencia (o transimpedancia) con la entrada en circuito abierto, respectivamente.
La Figura 2(a) muestra modelo eléctrico general de una red de dos puertos en función de sus parámetros de impedancia, mientras que la Figura 2(b) muestra el modelo de tipo "T" para redes pasivas recíprocas.
 |
| Fig. 2. Modelos de parámetros Z: (a) Modelo general y (b) Modelo e "T" para redes pasivas recíprocas |
La matriz [Y] se puede descomponer en dos ecuaciones:
A partir de estas ecuaciones es posible definir el significado de los términos yij de la matriz procediendo de forma análoga a la que se ha utilizado para determinar los parámetros de impedancia de red:
Los términos y11 y y21 se determinan con el puerto de salida en corto circuito (es decir, forzando v2 = 0), y excitando el puerto de entrada con un generador de corriente. Por ello se denominan admitancias de entrada con la salida en corto circuito y admitancia de transferencia (o transadmitancia) con la salida en corto circuito, respectivamente.
Los términos y22 y y12 se determinan con el puerto de entrada en corto circuito (es decir, forzando v1 = 0), y excitando el puerto de salida con un generador de corriente. Por ello se denominan admitancia de salida con la entrada en corto circuito y admitancia de transferencia (o transadmitancia) con la entrada en corto circuito, respectivamente.
La Figura 3(a) muestra modelo eléctrico general de una red de dos puertos en función de sus parámetros de admitancia, mientras que la Figura 3(b) muestra el modelo de tipo "Π" para redes pasivas recíprocas.
 |
| Fig. 3. Modelos de parámetros Y: (a) Modelo general y (b) Modelo e "Π" para redes pasivas recíprocas |
- Representación de parámetros híbridos (o parámetros h). En este modelo se eligen como variables independientes la corriente de entrada i1 y la tensión de salida v2 .
- Representación de parámetros híbridos inversos (o parámetros g). En este modelo se eligen como variables independientes la tensión de entrada v1 y la corriente de salida i2.
- Conexión serie-serie, en la que dos redes A y B, caracterizadas respectivamente por las matrices de impedancias [ZA] y [ZB] están conectadas de manera que el puerto "1" de ZA esté conectado en serie con el puerto "1" de ZB. Análogamente el puerto "2" de ZA está conectado en serie con el puerto "2" de ZB.
- Conexión paralelo-paralelo, en la que dos redes A y B, caracterizadas respectivamente por las matrices de admitancias [YA] y [YB] están conectadas de manera que el puerto "1" de YA esté conectado en serie con el puerto "1" de YB. Análogamente el puerto "2" de YA está conectado en serie con el puerto "2" de YB.
- Conexión en cascada, en la que el puerto "2" de una red A está conectado al puerto "1" de una red B.
 |
| Fig. 4. Topología de interconexión de redes: (a) serie-serie, (b) paralelo-paralelo, y (c) en cascada |
Observe que para una conexión de tipo serie-serie resulta:
Por otro lado, para una conexión de tipo paralelo-paralelo resulta:
Finalmente, para una conexión en cascada resulta:
Asimismo, existen también formas de conexión híbridas de tipo serie-paralelo y paralelo-serie.
Desafortunadamente, medir tensiones y corrientes en circuitos de radiofrecuencia es una operación poco práctica especialmente a frecuencias elevadas, por lo que se prefiere utilizar los parámetros scattering del dispositivo. Los parámetros scattering (o parámetros S) se utilizan extensivamente en las fases de modelado, diseño de las especificaciones y de circuitos de radiofrecuencias. Dichos parámetros pueden ser medidos de forma directa utilizando un analizador de redes y pueden ser relacionados directamente con los parámetros Z (impedancias) y Y (admitancias) de la red analizada. Para una red genérica de N puertas, la matriz S es dada por la siguiente ecuación:
siendo a1, a2, . . . , aN las ondas incidentes en los puertos 1, 2, . . .,N, respectivamente y b1, b1, . . . , bN las ondas reflejadas en estos mismos puertos. Estas ondas están definidas de manera que sean proporcionales a las tensiones incidentes y reflejadas y calculadas a partir de estas últimas, normalizándolas respecto a la raíz cuadrada de la impedancia característica (típicamente 50Ω). De esta manera, pues, |a|2 y |b|2 representan la potencia incidente y reflejada en un puerto del circuito.
Los parámetros S, pues, son por definición coeficientes complejos adimensionados ya que representan la relación entre tensiones normalizadas incidentes y reflejadas en cada puerto del circuito, y gozan de una serie de propiedades interesantes:
Los parámetros S, pues, son por definición coeficientes complejos adimensionados ya que representan la relación entre tensiones normalizadas incidentes y reflejadas en cada puerto del circuito, y gozan de una serie de propiedades interesantes:
- Para cada puerto j adaptado es sjj =0.
- Si la red es recíproca sij=sji.
- Para un circuito pasivo |sij|£1.
- Para una red recíproca sin pérdidas, en el puerto j genérico vale la siguiente relación:
es decir:
 |
| Fig. 5. Red de dos puertos y parámetros scattering |
Esta última propiedad significa que el producto de cada columna de la matriz S por el conjugado de la misma columna es igual a “1”. Desde el punto de vista energético esta relación afirma que la potencia total aplicada a un puerto j es igual a “1” y es en parte reflejada y en parte transmitida a los otros puertos de la red.
En el caso de la red de dos puertos que se muestra en la Figura 5, se obtiene la siguiente matriz scattering:
que puede descomponerse en las dos ecuaciones siguientes:
A partir de estas ecuaciones es posible definir el significado de los términos sij de la matriz:
El término s11 representa el coeficiente de reflexión Γ1 en el puerto "1" de la red medido con a2 = 0 (es decir con la terminación del circuito adaptada). El término s12 representa el coeficiente de transmisión inversa T12 del puerto "2" al puerto "1", medido con ambos puertos de la red adaptados. El término s21 representa el coeficiente de transmisión directa T21 del puerto "1" al "2", medido con ambos puertos de la red adaptados. Finalmente, el término s22 representa el coeficiente de reflexión en el puerto "2" de la red medido con a1 = 0 (es decir con el generador adaptado).
También es posible definir las pérdidas de retorno (return losses -RL), medidas en dB, como:
y las pérdidas de inserción (insertion losses -IL), también medidas en dB, como:
Finalmente, la rotación de fase introducida por la red es:

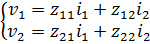











cual es tu bibliografia?
ResponderEliminarHola,
ResponderEliminares un resumen de un capítulo de un libro de RF que escribí hace unos años y que nunca llegué a publicar porque se me fue la mano y escribí más de mil páginas. De todas maneras esta información la puedes encontrar en un cualquier libro de teoría de circuitos. Por ejemplo:
1- Chua, Desoer, Kuh, "Linear and non linear circuits"
2- Desoer, Kuh 'Fundamentals of Circuit Theory'
3- Sadiku, 'Fyndamentals of electric circuits'