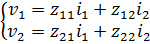Sobre la Ganancia de una Red de dos Puertos

Fig. 1. Red de dos puertos

En mi artículo anterior expliqué cómo estudiar la estabilidad de un amplificador a partir de sus parámetros scattering utilizando la carta de Smith y los círculos de estabilidad. Asimismo, demostré con un ejemplo práctico cómo aplicar deforma muy intuitiva esta técnica para diseñar un amplificador estable en el rango de frecuencias de interés.

En este nuevo artículo me centraré en otro aspecto fundamental del diseño de sistemas de radiofrecuencia: la ganancia de potencia. Seguiré considerando el transistor como una "caja negra" modelada por sus parámetros scattering a la frecuencia de interés e introduciré una serie de figuras de mérito para llegar a diseñar redes de adaptación de impedancia que permitan maximizar la potencia entregada a la carga.

La ganancia (o atenuación) de una red de dos puertos, como la que se muestra en la Figura 1, puede deducirse comparando la potencia entrante P₁ en la red y la potencia P_L que sale de la red y se disipa en la carga y pueden definirse como:

Donde V₁ = Z₁I₁, V₂ = Z_LI₂ , y las partes reales de las impedancias de entrada y de carga R₁ = Re{Z₁}, R_L =Re{ Z_L}.

La máxima potencia que la fuente puede entregar a una carga se denomina potencia disponible (available power) de la fuente P_avS y se obtiene cuando se realiza una adaptación conjugada entre carga y fuente de señal; es decir, P_avS = P₁ cuando Z₁ = Z*_G.

De forma análoga es posible definir la potencia disponible de la red de dos puertos P_avL, es decir, la máxima potencia que la red puede entregar a una carga. Esta condición se da cuando existe adaptación conjugada entre el puerto de salida de la red y la impedancia de carga; en otras palabras, P_avL = P_L cuando Z_L = Z*₂.

La potencia disponible puede expresarse en función de la impedancia característica y de los coeficientes de reflexión en le fuente y en la carga:

Tres definiciones muy útiles para la ganancia de potencia de una red de dos puertos son la ganancia de potencia de transducción G_T, la ganancia de potencia disponible G_a, y la ganancia de potencia G_p, conocida también como ganancia operativa. Estas potencias se definen como se muestra a continuación:

Estas ganancias pueden expresarse en términos de parámetros scattering:

La ganancia de potencia de transducción G_T  es probablemente la medida de ganancia de una red de  dos puertos más representativa porque incorpora los efectos de las impedancias de fuente y carga, mientras que G_a depende sólo de la impedancia de fuente y G_p depende sólo de la impedancia de carga.

El caso de la ganancia de potencia de transducción se representa en la Figura 2, en la que una fuente y una carga con la misma impedancia característica Z₀ están adaptadas a la red de dos puertos mediante dos redes de adaptación genéricas cuyos coeficientes de reflexión están representados en la figura.

Fig. 2. Estructura de la red de dos puertos para el cálculo de G_T

La expresión de G_T obtenida previamente puede expresarse de forma alternativa con unas manipulaciones algebraicas del denominador muy sencillas. Poniendo a factor común (1-s₂₂Γ_L ) y observando que:

se obtiene:

De forma análoga, poniendo a factor común (1-s₁₁Γ_S ) y observando que:

se obtiene:

De todas maneras, independientemente de la forma en la que es posible expresar la ganancia de transducción G_T, su expresión resultará siempre dependiente (directa o indirectamente)  de los coeficientes de reflexión Γ_S y Γ_L que resultan ser pues parámetros arbitrarios.

Para calcular la ganancia operativa G_p hay que considerar la red que se representa en la Figura 3, en la que la red de adaptación de impedancia de entrada es diseñada de manera que se realice  una adaptación de tipo conjugado entre la fuente de señal y la red de dos puertos; es decir,  Γ_S = Γ*₁. En otras palabras, la ganancia operativa es la ganancia de un dispositivo bajo la asunción de adaptación conjugada en el puerto de entrada y de una adaptación arbitraría en el puerto de salida que permita alcanzar la ganancia deseada.

Fig. 3. Estructura de la red de dos puertos para el cálculo de G_p

La expresión de la ganancia operativa G_p se obtiene pues de la ganancia de transducción G_T sustituyendo la condición de adaptación de impedancia del puerto de entrada de la red; es decir, imponiendo en la expresión de G_T la condición Γ_S = Γ*₁. Queda evidente que en este caso la expresión de la ganancia es independiente de Γ_S y el único parámetro arbitrario es el coeficiente de reflexión en la carga Γ_L.

La expresión de la ganancia operativa G_p obtenida con anterioridad puede reescribirse de forma alternativa sustituyendo la expresión de Γ₁ y realizando una serie de simples manipulaciones algebraicas sobre el denominador de la función, obteniendo:

Donde Δ=s₁₁s₂₂-s₁₂s₂₁.

Para calcular la ganancia de potencia disponible G_a hay que considerar la red que se representa en la Figura 4, en la que la red de adaptación de impedancia de salida es diseñada de manera que se realice una adaptación de tipo conjugado entre la red de dos puertos y la impedancia de carga; es decir, Γ_L = Γ*₂. En otras palabras, la ganancia de potencia disponible es la ganancia de un dispositivo bajo la asunción de adaptación conjugada en el puerto de salida y de una adaptación arbitraria en el puerto de entrada que permita alcanzar la ganancia deseada.

Fig. 4. Estructura de la red de dos puertos para el cálculo de G_a

La expresión de la ganancia de potencia disponible G_a se obtiene pues de la ganancia de transducción G_T sustituyendo la condición de adaptación de impedancia del puerto de salida de la red; es decir, imponiendo en la expresión de G_T la condición Γ_L = Γ*₂. Queda evidente que en este caso la expresión de la ganancia es independiente de Γ_L y el único parámetro arbitrario es el coeficiente de reflexión en la carga Γ_S.

La expresión de la ganancia de potencia disponible G_a obtenida con anterioridad puede reescribirse de forma alternativa sustituyendo la expresión de Γ₂ y realizando una serie de simples manipulaciones algebraicas sobre el denominador de la función, obteniendo:

Donde Δ=s₁₁s₂₂-s₁₂s₂₁.

Si un circuito es potencialmente inestable una adaptación de tipo conjugado podría no ser posible (es este el caso en que la impedancia conjugada cae en la región de inestabilidad). En este caso hay que optar por una adaptación arbitraria evitando de entrar en una región de inestabilidad.

Si las impedancias de fuente y carga están adaptadas a la impedancia de referencia Z₀ de manera que Z_S=Z_L= Z₀, (es decir, cuando Γ_S = Γ_L = 0), Γ₁ = s₁₁, Γ₂ = s₂₂, entonces las ganancias de potencia se reducen a:

Una red de dos puertos unilateral tiene, por definición, un coeficiente de transmisión inverso igual a cero, es decir, s₁₂=0. También en este caso los coeficientes de reflexión en entrada y salida de la red calculados previamente se simplifican reduciéndose a Γ₁ = s₁₁ y Γ₂ = s₂₂. Por consiguiente, las expresiones  de las ganancias unilaterales resultan ser:

Tanto para el caso bilateral como para el unilateral, las ganancias G_a y G_p se pueden obtener de G_T imponiendo Γ_L = Γ*₂  y  Γ₁ = Γ*_S respectivamente.

Fig. 5. Estructura de la red de dos puertos para el cálculo de G_Tu

Para calcular la ganancia de potencia disponible G_a hay que considerar la red que se representa en la Figura 5 observando que la ganancia de transducción unilateral G_Tu puede expresarse como:

Donde G_S representa la ganancia de la red de adaptación entre red y fuente, G₀ la ganancia de la red de dos puertos, y G_L la ganancia de la red de adaptación de impedancia entre red de dos puertos y carga.

La máxima ganancia unilateral se alcanza mediante adaptación conjugada, es decir cuando Γ_S = s*₁₁ y Γ_L = s*₂₂, lo que lleva a los siguientes valores máximos para G_S, G_L y para la ganancia de transducción G_T:

Tal y como en el caso del problema de la estabilidad que traté en mi anterior artículo, también para abordar el problema de la transmisión de potencia entre una fuente de señal y una carga utilizando la carta de Smith. Es posible definir unos círculos de ganancia operativa constante de centro C_p y radio R_p definidos tal y como se muestra a continuación:

El término g_p representa la relación entre la ganancia G_p (expresada en valor absoluto) que se pretende alcanzar con la red de adaptación de impedancia y el cuadrado del módulo de la ganancia directa s₂₁ . Un círculo de ganancia operativa constante es, por tanto, el lugar geométrico de todas las posibles impedancias de carga que resultan en una ganancia operativa constante igual a G_p, cuando el puerto de entrada es adaptado de forma conjugada con la impedancia de la fuente de señal.

Fig. 6. Círculos de ganancia operativa
constante

La Figura 6 muestra los círculos de ganancia operativa constante ara tres posibles ganancias objetivo g₃<g₂<g₁. Observe como, al aumentar de la ganancia objetivo el radio del círculo de ganancia se reduce. El círculo que corresponde a la máxima ganancia operativa podría llegar a ser, en el caso de que fuera posible adaptación conjugada, simplemente un punto. La máxima ganancia operativa no puede exceder la máxima ganancia disponible G_MAG que  definiré más adelante.

Observe también que el centro C_p del círculo de ganancia es un número complejo y, por consiguiente, su módulo y fase identificarán de forma unívoca el centro del círculo de ganancia en el plano complejo. Tenga también presente que Re{C_p} no puede ser mayor que 1, por tanto el centro del círculo de ganancia cae siempre dentro la carta de Smith. Por otro lado, el radio R_p del círculo de ganancia en un número non negativo menor o igual a 1. Esto significa que pueden existir casos en los que parte del círculo de ganancia podría yacer fuera de la carta de Smith. Esto significa que algunas de las impedancias del círculo considerado tienen parte real negativa y llevan a un comportamiento inestable.

De forma análoga es posible definir unos círculos de ganancia disponible constante. Se trata del lugar geométrico de todas las posibles impedancias de fuente que resultan en una ganancia disponible constante G_a, cuando el puerto de salida es adaptado de forma conjugada con la impedancia de carga. Un círculo de ganancia disponible constante es caracterizado por un centro C_a y un radio R_a definidos tal y como se muestra a continuación:

Para el círculo de ganancia disponible constante valen exactamente las mismas consideraciones hechas por el círculo de ganancia operativa constante.

La ganancia de transducción es maximizada cuando los dos puertos de la red están adaptados simultáneamente de forma conjugada con fuente y carga, es decir, cuando Γ_L = Γ*₂  y  Γ₁ = Γ*_S. En estas condiciones las tres ganancias son iguales y es posible definir una máxima ganancia común obtenida por la adaptación conjugada simultánea de los puertos de entrada y salida de la red que se conoce también como máxima ganancia disponible (Maximum Available Gain –MAG) :

G_T,max = G_a,max = G_p,max = G_MAG

La condición necesaria y suficiente para la adaptación simultánea de los puertos de la red es K ≥ 1, siendo K el factor de estabilidad de Stern (introducido en mi artículo anterior sobre la estabilidad de redes de dos puertos). Se puede demostrar que el MAG puede expresarse como:

Si K£1 la red de dos puertos es potencialmente inestable y no es posible garantizar la adaptación conjugada simultánea de los puertos de entrada y salida de la red ya que una (o incluso ambas) de las impedancias conjugadas podría caer dentro de una región de inestabilidad de la carta de Smith. Esto no significa en absoluto que el circuito no pueda realizarse físicamente, sino que hay que realizar un tipo de adaptación arbitrario en unos o ambos puertos del circuito. Obviamente, para circuitos potencialmente inestables, la definición anterior de G_MAG no es válida y hay que buscar una definición alternativa de ganancia.

La máxima ganancia estable (Maximum Stable Gain –MSG) es la MAG calculada para K£1, es decir:

En el caso de un dispositivo unilateral, el MAG se obtiene imponiendo Γ_S = Γ*₁= s*₁₁ y  Γ_L = Γ*₂= s*₂₂ en las expresiones de las ganancias unilaterales:

A menudo, las redes de dos puertos como los transistores a las radiofrecuencias o a las microondas son aproximadamente unilaterales, es decir, los parámetros scattering medidos cumplen con el requisitos |S₁₂|<<|S₂₁|. Para decidir si una red de dos puertos puede considerarse unilateral existe una figura de mérito que es, en su esencia, una comparación entre la máxima ganancia unilateral y la ganancia del transductor de un dispositivo bajo las mismas condiciones de adaptación de impedancia; es decir, Γ_S = s*₁₁ y  Γ_L = s*₂₂. Para estos valores adaptados de Γ_S  y  Γ_L, la relación entre las ganancias de transductor unilateral y bilateral es de la forma:

La cantidad |U| se conoce con el nombre de figura de mérito unilateral. Si el ratio de ganancia relativa g_u es aproximadamente unitario (típicamente dentro de un rango de variación del ±10% de la unidad), la red de dos puertos puede tratarse como una red unilateral, es decir, debe ser:

Finalmente, es posible definir unos círculos de ganancia unilateral constante tanto para el plano de la fuente como para el plano de la carga. Los círculos de ganancia unilateral constante en el plano de la fuente tienen, respectivamente un radio R_Su y un centro C_Su definidos de la siguiente manera:

Análogamente, un círculo de ganancia unilateral constante en el plano de carga es caracterizado por los siguientes valores de radio y centro de la circunferencia:

Algunas Reflexiones sobre la Estabilidad de los Transistores

Cuando se diseña un amplificador, el objetivo principal es evitar que el circuito se vuelva inestable produciendo oscilaciones no deseadas. La técnica estándar que se utiliza para diseñar circuitos estables se basa en calcular una figura de mérito conocida como factor K, que equivale a determinar sobre la carta de Smith los que se conocen como círculos de estabilidad.

Los orígenes del factor K pueden remontarse al artículo de J. M. Rollet "Stability and Power-Gain Invariants of Linear Twoports” publicado en la IRE Transactions on Circuit Theory en marzo de 1962. Por ello, muchos se refieren a este factor como factor de estabilidad de Rollet. No obstante, en su artículo, Rollet se limitó a realizar algunas transformaciones matemáticas sobre una expresión previamente derivada por A. P. Stern en 1957. Por esta razón, otros, entre los que me incluyo yo también, se refieren al factor K como factor de estabilidad de Stern. 

Cabe remarcar que la ecuación derivada en su tiempo por Stern y revisitada por Rollet no se expresó, como es común hoy en día, en función de los parámetros scattering del dispositivo. El criterio de estabilidad comúnmente aceptado y utilizado en la actualidad consiste en comprobar el valor de dos factores:

K > 1        |Δ|<1

Siendo K el factor de estabilidad de Stern, definido como:

y Δ=det(S) el determinante de la matriz scattering S; es decir:

El cumplimiento  de estos criterios garantiza, en la mayor parte de los casos, que la red de dos puertos analizada sea incondicionalmente  estable; aunque es probable que lleven a conclusiones equivocadas en el caso de amplificadores multietapa con topologías complejas.

Existen criterios alternativos al anterior, que, sin embargo gozan de menor aceptación, para determinar la estabilidad de una red lineal de dos puertos. Uno de los más conocidos es el criterio de Edwards y Sinsky, que consiste en determinar uno entre dos factores de estabilidad, μ₁ o μ₂, respectivamente en el puerto de entrada de la red lineal o en el puerto de salida de la red):

y comprobar que  μ₁>1 o, equivalentemente μ₂>1. Sin embargo, también este criterio puede derivarse a partir del criterio de estabilidad de Stern.

Fig. 1.  Conexión de una red lineal con una fuente y una carga

Cuando una red lineal de dos puertos se conecta a una fuente y a una carga tal y como se muestra en la Figura 1 es posible expresar el coeficiente de reflexión Γ₁ en el puerto de entrada en función de los parámetros scattering de la red y del coeficiente de reflexión en la carga Γ_L=(Z_L-Z₀)/(Z_L+Z₀). De forma análoga es posible expresar el coeficiente de reflexión Γ₂ en el puerto de salida en función de los parámetros scattering de la red y del coeficiente de reflexión en la fuente Γ_S=(Z_S-Z₀)/(Z_S+Z₀); es decir:

En general, una red de dos puertos es incondicionalmente estable si cualquiera impedancia de la fuente y de la carga con partes reales positivas R_S y R_L llevará siempre a una impedancias de entrada y de salida (es decir, las impedancias Z₁ y Z₂ que se ven respectivamente desde los puertos "1" y "2" de la red de dos puertos) con partes reales positivas R₁ y R₂ respectivamente. De forma equivalente, los requisitos para la estabilidad incondicional se pueden expresar también en función de los coeficientes de reflexión. La estabilidad incondicional requiere que cualquier cargas y fuentes con |Γ_L|<1 y |Γ_S|<1 resulte en |Γ₁|<1 y |Γ₂|<1.

Por otro lado, una red de dos puertos se denomina potencialmente o condicionalmente inestable si existen algunos valores de cargas y fuentes con |Γ_L|<1 y |Γ_S|<1 que resultan en |Γ₁|≥ 1 y |Γ₂|≥ 1.

Fig. 2. Círculo de estabilidad

La región de estabilidad de carga es el conjunto de todos los Γ_L que resultan en |Γ₁|<1 y la región de estabilidad de fuente es el conjunto de todos los Γ_S que resultan en |Γ₂|<1. En el caso de estabilidad incondicional, las regiones de estabilidad de fuente y carga contienen completamente los círculos de radio unitario |Γ_L|<1 y |Γ_S|<1. Sin embargo, en el caso de una configuración potencialmente inestable, sólo unas porciones del círculo de radio unitario puede hallarse en la región de estabilidad, por tanto sólo aquellos valores de Γ_L y Γ_S que se hallan en la región de estabilidad llevarán a una impedancias de fuente y de carga estables.

La Figura 2 muestra el significado geométrico de los círculos y las regiones de estabilidad. El círculo de estabilidad puede definirse tanto para una impedancia fuente como para la impedancia de carga. En el caso de una impedancia de carga, el círculo de estabilidad tiene un radio r_L y un centro C_L definido respecto al centro de la carta de Smith (por tanto se trata, tal y como se muestra en la Figura 2, de un número complejo) . Los valores de r_L y C_L pueden calcularse a partir de los parámetros scattering del dispositivo tal y como se muestra a continuación:

De forma análoga es posible definir los círculos de estabilidad de fuente con radio r_S y C_S respectivamente:

Los círculos de estabilidad definen una región de estabilidad que puede ser interna o externa al círculo. En en caso de los círculos de estabilidad de carga, la región de estabilidad es:

• externa al círculo de estabilidad (es decir, |Γ_L-C_L|>r_L) si |s₂₂|²-|Δ|²>0;
• interna al círculo de estabilidad (es decir, |Γ_L-C_L|<r_L) si |s₂₂|²-|Δ|²<0.

En el caso de los círculos de estabilidad de fuente, la región de estabilidad es:

• externa al círculo de estabilidad (es decir, |Γ_S-C_S|>r_S) si |s₁₁|²-|Δ|²>0;
• interna al círculo de estabilidad (es decir, |Γ_S-C_S|<r_S) si |s₁₁|²-|Δ|²<0.

El contorno del círculo corresponde al caso en que el coeficiente de reflexión (en el puerto de entrada o de salida, dependiendo de si se está considerando el círculo de fuente o de carga) vale 1. La región complementaria corresponde al caso en el que el coeficiente de reflexión es mayor que 1 (es decir, la región inestable).

Por consiguiente, la región estable se halla dentro del círculo de estabilidad cuando el centro de la carta de Smith cae dentro del círculo y fuera del círculo de estabilidad en caso contrario. Si el círculo cae completamente fuera de la carta de Smith o lo contienen completamente la red de dos puertos es incondicionalmente estable. Todas estas situaciones se representan en la Figura 3.

Figura 3. Círculos y regiones de estabilidad. Las Figuras (b) y (c) representan los dos casos de redes de dos puertos incondicionalmente estables. Las Figuras (a), (d), (e) y (f) representan redes de dos puertos potencialmente inestables

Si se consideran los círculos de estabilidad de carga, la Figura 3(c) representa el caso en que |C_L|-r_L>1 (el círculo de estabilidad no contiene el centro de la carta de Smith) y |s₂₂|²-|Δ|²>0, la Figura 3(b) representa el caso en que r_L-|C_L|>1 (el círculo de estabilidad contiene el centro de la carta de Smith)y |s₂₂|²-|Δ|²<0, las Figuras 3(a) y 3(e) representan el caso en que |C_L|-r_L<1 y |s₂₂|²-|Δ|²>0; finalmente, las Figuras 3(d) y 3(f) representan el caso en que r_L-|C_L|<1 y |s₂₂|²-|Δ|²<0.

La Diferencia Fundamental entre Parámetros Scattering y Modelos Spice

En este artículo voy a hacer hincapié en las diferencias fundamentales entre parámetros scattering y modelos spice. 

Existen muchos tipos de modelos spice con distintos tipos de precisión de modelado y orientados a representar el comportamiento de dispositivos de diferentes tipos en distintos rangos de tensiones, corrientes y temperaturas operativas. Por ejemplo, tanto en Electrónica II como en Diseño de Circuitos y Sistema Electrónicos, se ha hecho mucho énfasis en el modelo spice de nivel 1 para MOSFETs (Metal-Oxide-Semiconductor Field Effect Transistor), un modelo muy sencillo pensado más para los cálculos manuales y dirigido al modelado de dispositivos de canal largo.

Este modelo sencillo se ha utilizado como punto de partida en Transmisión por Radiofrecuencia y se han investigado sus limitaciones en el caso de dispositivos de canal corto ampliándolo con un nuevo juego de ecuaciones que tengan en cuenta de uno de los efectos de canal corto (short channel effects) más importantes: la saturación de la velocidad de los portadores mayoritarios en el canal (velocity saturation).

Un modelo es pues, como se ha visto con mucho detalles en las clases teóricas, un conjunto de ecuaciones específicas para un dispositivo dado (transistor bipolar, transistor MOS, etc.) que operan sobre una serie de parámetros que dependen de la tecnología y que están incluidos en un fichero de modelo (en el caso de la asignatura Transmisión por Radiofrecuencia se utiliza, por ejemplo, un modelo spice de nivel 8 para un proceso de fabricación de 0.35μm cuyo parámetros se hallan en el fichero de tecnología Trf_035.lib que se halla en la carpeta compartida de OpenClass con el material del curso).

Cada modelo disponible está orientado a modelar el comportamiento de un dispositivo en condiciones operativas distintas. Por ejemplo, algunos modelos sencillos asumen condiciones operativas estáticas, es decir, están orientados a capturar el comportamiento del dispositivo asumiendo que las condiciones de polarización (las tensiones en los bornes del dispositivo) se mantienen constantes con el tiempo; otros modelos, orientados más al modelado de dispositivos de potencia (que manejan señales grandes y tienen un comportamiento fuertemente no lineal) pueden incluir otros efectos como constante de tiempo e inercia térmicas.

Por otro lado, los parámetros scattering (S-parameters) son algo completamente diferente se trata de una serie de datos (data set), normalmente medidos de forma experimental, que "capturan" el comportamiento de un dispositivo dado para unas condiciones de polarización (tensión en sus bornes y corrientes) específicas a distintas frecuencias operativas. Por consiguiente, para realizar un modelado completo utilizando parámetros scattering es necesario disponer de distintos data sets calculados para todas las posibles condiciones operativas de un dispositivo. Existen herramientas de diseño que permiten extraer un modelo spice, es decir, una serie de parámetros del modelo, que se ajusta con mayor o menor precisión a los parámetros scattering medidos experimentalmente.  La precisión del modelo spice derivado depende pues del tamaño del data set utilizado para realizar la extracción. Obviamente, si el tamaño del data set es pequeño, el modelo spice obtenido sirve sólo para tener unos resultados cualitativos para condiciones de funcionamiento típicas de un dispositivo, pero pueden resultar poco adecuadas para predecir su funcionamiento en condiciones de máximos y mínimos. Para obtener modelos de dispositivos reales que permitan el modelado de todos sus efectos no lineales en todas las posibles condiciones operativas, es necesario extrapolar el modelo spice a partir de un data set muy grande.

Utilizar parámetros scattering permite representar en spice un circuito o dispositivo mediante una "caja negra", es decir como una red lineal de dos puertos que representa el comportamiento especificado por el data set asociado.  Esta técnica suele dar muy buenos resultados para circuitos pasivos y menos buenos para dispositivos activos.

Sobre Redes de Dos Puertos y Parámetros Scattering

Un puerto, por definición, es un par de terminales a través de las cuales es posible que entre o salga corriente de una red o un dispositivo. Dispositivos de dos terminales como las resistencias, los condensadores y los inductores son redes de un puerto. En general, una red puede tener n puertos. Cada puerto de acceso a la red consta de un par de terminales. La corriente que entra en una terminal sale a través del otro, de modo que la corriente neta que entra en un puerto es igual a cero. 

De particular relevancia son las las redes de dos puertos, es decir, circuitos (como por ejemplo filtros activos y pasivos y amplificadores) en que se define un par de terminales como puerto de entrada y otro par de terminales como puerto de salida. Una red de dos puertos puede conectarse con un generador o una carga tal y como se muestra, por ejemplo, en la Figura 1. También puede conectarse con otra red de dos puertos para constituir una red de dos puertos más compleja.

Fig. 1. Red Lineal de 2 Puertos

Una red lineal de n puertos puede ser descrita mediante un sistema de n ecuaciones lineales. Una red de dos puertos como la que se muestra en la Figura 1, por ejemplo, puede ser caracterizada a través de su impedancia o su admitancia. Por ejemplo, la relación entre corrientes y tensiones dada por la ley de Ohm se puede expresar en forma matricial tal y como se muestra a continuación:

siendo v₁ e i₁ la tensión y la corriente en el puerto “1”, y v₂ e i₂ la tensión y la corriente en el puerto “2” de la red de dos puertos. Los términos z_ij representan la relación entre entrada y salida del circuito; en particular, el índice j indica la puerta en que se aplica una señal, mientras que el índice i indica el puerto donde se observa una señal. La red se define simétrica cuando z₁₁= z₂₂, y recíproca cuando z₁₂ = z₂₁.

La matriz [Z] se puede descomponer en dos ecuaciones:

A partir de estas ecuaciones es posible definir el significado de los términos z_ij de la matriz:

Los términos z₁₁ y z₂₁ se determinan dejando el puerto de salida en circuito abierto (es decir, forzando i₂ = 0), y excitando el puerto de entrada con un generador de tensión. Por ello se denominan impedancia de entrada con la salida en circuito abierto e impedancia de transferencia (o transimpedancia) con la salida en circuito abierto, respectivamente.


Los términos z₂₂ y z₁₂ se determinan dejando el puerto de entrada en circuito abierto (es decir, forzando i₁ = 0), y excitando el puerto de salida con un generador de tensión. Por ello se denominan impedancia de salida con la entrada en circuito abierto e impedancia de transferencia (o transimpedancia) con la entrada en circuito abierto, respectivamente.

La Figura 2(a) muestra modelo eléctrico general de una red de dos puertos en función de sus parámetros de impedancia, mientras que la Figura 2(b) muestra el modelo de tipo "T" para redes pasivas recíprocas.

Fig. 2. Modelos de parámetros Z: (a) Modelo general y (b) Modelo e "T" para redes pasivas recíprocas

Una representación alternativa se basa en la admitancia y del dispositivo, por lo que se puede escribir:

La matriz [Y] se puede descomponer en dos ecuaciones:

A partir de estas ecuaciones es posible definir el significado de los términos y_ij de la matriz procediendo de forma análoga a la que se ha utilizado para determinar los parámetros de impedancia de red:

Los términos y₁₁ y y₂₁ se determinan con el puerto de salida en corto circuito (es decir, forzando v₂ = 0), y excitando el puerto de entrada con un generador de corriente. Por ello se denominan admitancias de entrada con la salida en corto circuito y admitancia de transferencia (o transadmitancia) con la salida en corto circuito, respectivamente.

Los términos y₂₂ y y₁₂ se determinan con el puerto de entrada en corto circuito (es decir, forzando v₁ = 0), y excitando el puerto de salida con un generador de corriente. Por ello se denominan admitancia de salida con la entrada en corto circuito y admitancia de transferencia (o transadmitancia) con la entrada en corto circuito, respectivamente.

La Figura 3(a) muestra modelo eléctrico general de una red de dos puertos en función de sus parámetros de admitancia, mientras que la Figura 3(b) muestra el modelo de tipo "Π" para redes pasivas recíprocas.

Fig. 3. Modelos de parámetros Y: (a) Modelo general y (b) Modelo e "Π" para redes pasivas recíprocas

Existen otras representaciones alternativas de redes de dos puertos entre las que cabe mencionar:

• Representación de parámetros híbridos (o parámetros h). En este modelo se eligen como variables independientes la corriente de entrada i₁  y la tensión de salida v₂ . 
• Representación de parámetros híbridos inversos (o parámetros g). En este modelo se eligen como variables independientes la tensión de entrada v₁ y la corriente de salida i₂. 

Las redes de dos puertos pueden conectarse de varias formas para formar redes más complejas. Las topologías más utilizadas se muestran el la Figura 4 y son:

• Conexión serie-serie, en la que dos redes A y B, caracterizadas respectivamente por las matrices de impedancias [Z_A] y [Z_B] están conectadas de manera que el puerto "1" de Z_A esté conectado en serie con el puerto "1" de Z_B. Análogamente el puerto "2" de Z_A está conectado en serie con el puerto "2" de Z_B.
• Conexión paralelo-paralelo, en la que dos redes A y B, caracterizadas respectivamente por las matrices de admitancias [Y_A] y [Y_B] están conectadas de manera que el puerto "1" de Y_A esté conectado en serie con el puerto "1" de Y_B. Análogamente el puerto "2" de Y_A está conectado en serie con el puerto "2" de Y_B.
• Conexión en cascada, en la que el puerto "2" de una red A está conectado al puerto "1" de una red B.

Fig. 4. Topología de interconexión de redes: (a) serie-serie, (b) paralelo-paralelo, y (c) en cascada

Observe que para una conexión de tipo serie-serie resulta:

Por otro lado, para una conexión de tipo paralelo-paralelo resulta:

Finalmente, para una conexión en cascada resulta:

Asimismo, existen también formas de conexión híbridas de tipo serie-paralelo y paralelo-serie.

Desafortunadamente, medir tensiones y corrientes en circuitos de radiofrecuencia es una operación poco práctica especialmente a frecuencias elevadas, por lo que se prefiere utilizar los parámetros scattering del dispositivo. Los parámetros scattering (o parámetros S) se utilizan extensivamente en las fases de modelado, diseño de las especificaciones y de circuitos de radiofrecuencias. Dichos parámetros pueden ser medidos de forma directa utilizando un analizador de redes y pueden ser relacionados directamente con los parámetros Z (impedancias) y Y (admitancias) de la red analizada. Para una red genérica de N puertas, la matriz S es dada por la siguiente ecuación:

siendo a₁, a₂, . . . , a_N  las ondas incidentes en los puertos 1, 2, . . .,N, respectivamente y b₁, b₁, . . . , b_N las ondas reflejadas en estos mismos puertos. Estas ondas están definidas de manera que sean proporcionales a las tensiones incidentes y reflejadas y calculadas a partir de estas últimas, normalizándolas respecto a la raíz cuadrada de la impedancia característica (típicamente 50Ω). De esta manera, pues, |a|² y |b|² representan la potencia incidente y reflejada en un puerto del circuito.

Los parámetros S, pues, son por definición coeficientes complejos adimensionados ya que representan la relación entre tensiones normalizadas incidentes y reflejadas en cada puerto del circuito, y gozan de una serie de propiedades interesantes:

• Para cada puerto j adaptado es s_jj =0.
• Si la red es recíproca s_ij=s_ji.
• Para un circuito pasivo |s_ij|£1.
• Para una red recíproca sin pérdidas, en el puerto j genérico vale la siguiente relación:

es decir:

Fig. 5. Red de dos puertos y parámetros scattering

Esta última propiedad significa que el producto de cada columna de la matriz S por el conjugado de la misma columna es igual a “1”. Desde el punto de vista energético esta relación afirma que la potencia total aplicada a un puerto j es igual a “1” y es en parte reflejada y en parte transmitida a los otros puertos de la red.

En el caso de la red de dos puertos que se muestra en la Figura 5, se obtiene la siguiente matriz scattering:

que puede descomponerse en las dos ecuaciones siguientes:

A partir de estas ecuaciones es posible definir el significado de los términos  s_ij de la matriz:

El término s₁₁ representa el coeficiente de reflexión Γ₁ en el puerto "1" de la red medido con a₂ = 0 (es decir con la terminación del circuito adaptada). El término s₁₂ representa el coeficiente de transmisión inversa T₁₂ del puerto "2" al puerto "1", medido con ambos puertos de la red adaptados. El término s₂₁ representa el coeficiente de transmisión directa T₂₁ del puerto "1" al "2", medido con ambos puertos de la red adaptados. Finalmente, el término s₂₂ representa el coeficiente de reflexión en el puerto "2" de la red medido con a₁ = 0 (es decir con el generador adaptado). 

También es posible definir las pérdidas de retorno (return losses -RL), medidas en dB, como:

y las pérdidas de inserción (insertion losses -IL), también medidas en dB, como:

Finalmente, la rotación de fase introducida por la red es: